Advertisements
Advertisements
प्रश्न
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
उत्तर
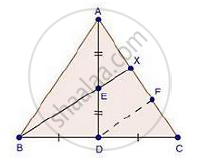
Given: In ΔABC, D is the mid-point of BC and E is the mid-point of AD.
To prove: BE : EX = 3 : 1
Const: Through D, draw DF || BX
Proof: In ΔEAX and ΔADF
∠EAX = ∠ADF [Common]
∠AXE = ∠DAF [Corresponding angles]
Then, ΔAEX ~ ΔADF [By AA similarity]
`therefore"EX"/"DF"="AE"/"AD"` [Corresponding parts of similar Δ are proportional]
`rArr"EX"/"DF"="AE"/"2AE"` [AE = ED given]
⇒ DF = 2EX …. (i)
In ΔCDF and ΔCBX [By AA similarity]
`therefore"CD"/"CB"="DF"/"BX"` [Corresponding parts of similar Δ are proportional]
`rArr1/2="DF"/"BE + EX"` [BD = DC given]
⇒ BE + EX = 2DF
⇒ BE + EX = 4EX
⇒ BE = 4EX – EX [By using (i)]
⇒ BE = 4EX – EX
`rArr"BE"/"EX"=3/1`
APPEARS IN
संबंधित प्रश्न
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
State the two properties which are necessary for given two triangles to be similar.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).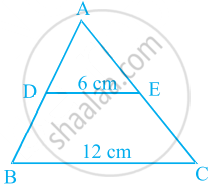
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
