Advertisements
Advertisements
प्रश्न
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
पर्याय
6 cm
7 cm
8 cm
9 cm
उत्तर
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = 8 cm.
Explanation:
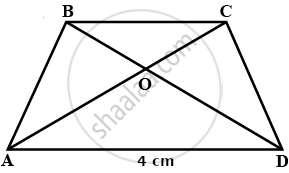
In ΔAOD and ΔBOC
∠AOD = ∠BOC .....(Vertically opposite angle)
`(AO)/(OC) = (DO)/(OB)` ......(Given)
∴ ΔAOD ∼ΔBOC ......(SAS similarity)
Since both triangles are similar.
Their sides will be in proportion
`(AO)/(OC) = (DO)/(OB) = (AD)/(BC)`
`1/2 = (AD)/(BC)`
Putting AD = 4 cm
`1/2 = 4/(BC)`
BC = 2 × 4
BC = 8 cm
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.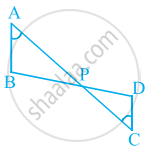
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
