Advertisements
Advertisements
Question
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
Options
6 cm
7 cm
8 cm
9 cm
Solution
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = 8 cm.
Explanation:
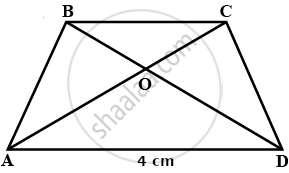
In ΔAOD and ΔBOC
∠AOD = ∠BOC .....(Vertically opposite angle)
`(AO)/(OC) = (DO)/(OB)` ......(Given)
∴ ΔAOD ∼ΔBOC ......(SAS similarity)
Since both triangles are similar.
Their sides will be in proportion
`(AO)/(OC) = (DO)/(OB) = (AD)/(BC)`
`1/2 = (AD)/(BC)`
Putting AD = 4 cm
`1/2 = 4/(BC)`
BC = 2 × 4
BC = 8 cm
APPEARS IN
RELATED QUESTIONS
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?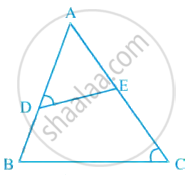
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

Which of the following is NOT a similarity criterion of traingles?
