Advertisements
Advertisements
Question
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
Solution
Given l || m and line segments AB, CD and EF are concurrent at point P.
To prove: `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Proof: In ΔAPC and ΔBPD,
∠APC = ∠BPD ...[Vertically opposite angles]
∠PAC = ∠PBD ...[Alternative angles]
∴ ΔAPC ∼ ΔBPD ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AC")/("BD") = ("PC")/("PD")` ...(i)
In ΔAPE and ΔBPF,
∠APE = ∠BPF ...[Vertically opposite angles]
∠PAE = ∠PBF ...[Alternative angles]
∴ ΔAPE ∼ ΔBPF ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AE")/("BF") = ("PE")/("PF")` ...(ii)
In ΔPEC and ΔPFD,
∠EPC = ∠FPD ...[Vertically opposite angles]
∠PCE = ∠PDF ...[Alternative angles]
∴ ΔPEC ∼ ΔPFD ...[By AA similarity criterion]
Then, `("PE")/("PF") = ("PC")/("PD") = ("EC")/("FD")` ...(iii)
From equations (i), (ii) and (iii),
`("AP")/("PB") = ("AC")/("BD") = ("AE")/("BF") = ("PE")/("PF") = ("EC")/("FD")`
∴ `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
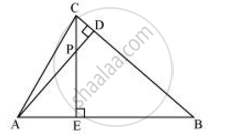
ΔAEP ∼ ΔCDP
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
State the AAA-similarity criterion
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.