Advertisements
Advertisements
Question
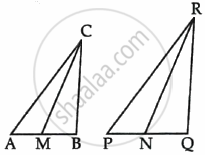
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
Solution
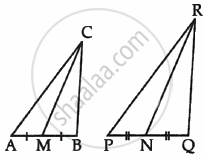
Given: ΔABC ∼ ΔPQR
and CM and RN are medians of ΔABC and ΔPQR respectively.
To Prove: ΔAMC ∼ ΔPNR
Proof: ΔABC ∼ ΔPQR ...(Given)
∴ ∠A = ∠P,
and `(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)`
`(AB)/(PQ) = (AC)/(PR)`
`(2AM)/(2PN) = (AC)/(PR)`
`(AM)/(PN) = (AC)/(PR)`
and ∠A = ∠P
∴ ΔAMC ∼ ΔPQR ...(SAS Test)
Hence Proved.
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

