Advertisements
Advertisements
Question
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

Solution
Given: ∠PQR = 90° and QS ⊥ PR.
So, ∠QSR = ∠QSP = 90°
Now, in ΔPQR and ΔQSR,
∠QRP ≅ ∠SRQ ......[Common angle]
∠PQR ≅ ∠QSR ......[Each angle is equal to 90°]
So, according to the AA similarity criterion,
ΔPQR ∼ ΔQSR
∴ `(PR)/(QR) = (PQ)/(QS)` .....[C.S.S.T.]
⇒ `r/q = p/x`
⇒ x × r = p × q
⇒ pq = rx
Hence proved.
APPEARS IN
RELATED QUESTIONS
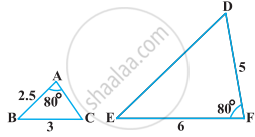
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
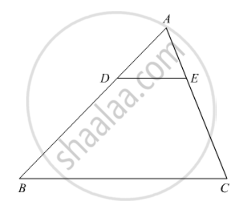
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
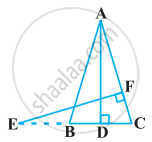
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
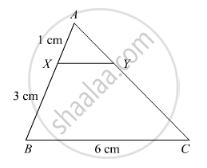
In the following figure, XY || BC. Find the length of XY.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
In the given figure, value of x(in cm) is

In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.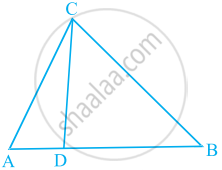
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
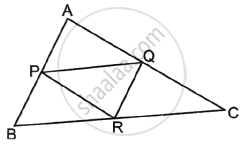
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
Which of the following is NOT a similarity criterion of traingles?
