Advertisements
Advertisements
Question
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
Solution
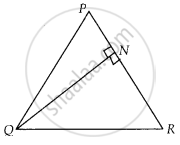
Given, ∆PQR,
N is a point on PR, such that QN ⊥ PR
And PN . NR = QN2
To prove: ∠PQR = 90°
Proof: We have, PN . NR = QN2
⇒ PN . NR = QN . QN
⇒ `("PN")/("QN") = ("QN")/("NR")` ...(i)
In ∆QNP and ∆RNQ,
`("PN")/("QN") = ("QN")/("NR")`
And ∠PNQ = ∠RNQ ...[Each equal to 90°]
∴ ∆QNP ~ ∆RNQ ...[By SAS similarity criterion]
Then, ∆QNP and ∆RNQ are equiangulars.
i.e., ∠PQN = ∠QRN
⇒ ∠RQN = ∠QPN
On adding both sides, we get
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN ...(ii)
We know that, sum of angles of a triangle is 180°
In ∆PQR,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180° ...[∵ ∠QPR = ∠QPN and ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° ...[Using equation (ii)]
⇒ 2∠PQR = 180°
⇒ ∠PQR = `180^circ/2` = 90°
∴ ∠PQR = 90°
Hence proved.
RELATED QUESTIONS
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

