Advertisements
Advertisements
Question
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
Options
50°
30°
60°
100°
Solution
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to 100°.
Explanation:

From ∆APB and ∆CPD,
∠APB = ∠CPD = 50° ...(Since they are vertically opposite angles)
`("AP")/("PD") = 6/5` ...(i)
Also, `("BP")/("CP") = 3/2.5`
Or `("BP")/("CP") = 6/5` ...(ii)
From equations (i) and (ii),
We get,
`("AP")/("PD") = ("BP")/("CP")`
So, ∆APB ∼ ∆DPC ...[Using SAS similarity criterion]
∴ ∠A = ∠D = 30° ...[Since, corresponding angles of similar triangles]
Since, Sum of angles of a triangle = 180°,
In ∆APB,
∠A + ∠B + ∠APB = 180°
So, 30° + ∠B + 50° = 180°
Then, ∠B = 180° – (50° + 30°)
∠B = 180° – 80° = 100°
Therefore, ∠PBA = 100°
APPEARS IN
RELATED QUESTIONS
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
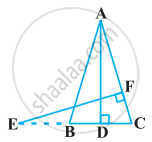
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.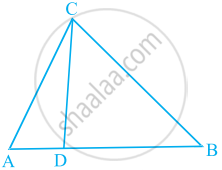
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
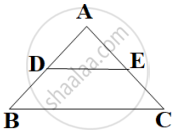
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

