Advertisements
Advertisements
Question
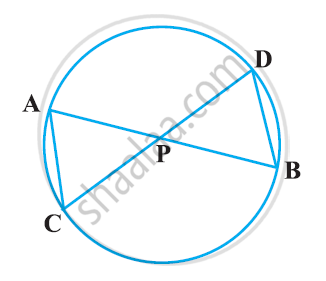
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

Solution
Given: Seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`.
To prove: ∆ABP ~ ∆CDP
Proof: In ∆ABP and ∆CDP,
`"AP"/"CP" = "BP"/"DP"` ...(Given)
∠APB ≅ ∠CPD ...(vertically opposite angles)
By SAS test of similarity,
∆ABP ~ ∆CDP
Hence Proved.
APPEARS IN
RELATED QUESTIONS
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
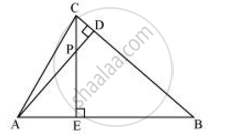
ΔAEP ∼ ΔCDP
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
ΔAEP ∼ ΔADB
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following figure, AB || QR. Find the length of PB.

D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

State the two properties which are necessary for given two triangles to be similar.
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.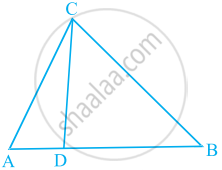
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?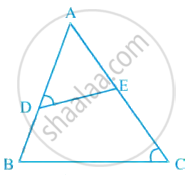
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.