Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board chapter 1 - Similarity [Latest edition]

Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.

In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find `("A"(∆"ABC"))/("A"(∆"ADB"))`

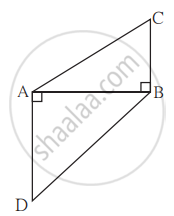
In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT. 

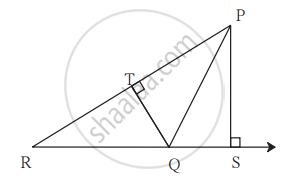
In the following figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD). 

In adjoining figure, PQ ⊥ BC, AD ⊥ BC then find following ratios.

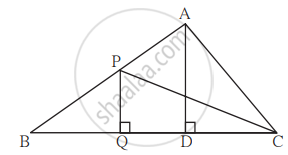
1. `("A"(∆"PQB"))/("A"(∆"PBC"))`
2. `("A"(∆"PBC"))/("A"(∆"ABC"))`
3. `("A"(∆"ABC"))/("A"(∆"ADC"))`
4. `("A"(∆"ADC"))/("A"(∆"PQC"))`

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

In ∆PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason. 

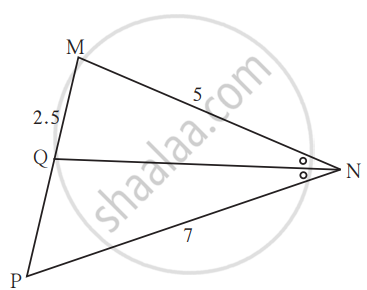
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP. 

Measures of some angles in the figure are given. Prove that `"AP"/"PB" = "AQ"/"QC"`.

In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ. 

Find QP using given information in the figure.

In the given figure, if AB || CD || FE then find x and AE. 

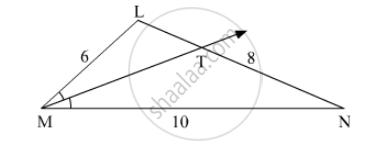
In ∆LMN, ray MT bisects ∠LMN If LM = 6, MN = 10, TN = 8, then Find LT. 

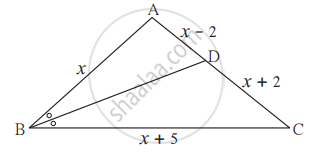
In ∆ABC, seg BD bisects ∠ABC. If AB = x, BC = x + 5, AD = x – 2, DC = x + 2, then find the value of x.

In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF. 

Proof :  In ΔXDE, PQ || DE         ...`square`

∴ `"XP"/square = square/"QE"`                               ...(I) (Basic proportionality theorem)

In ΔXEF, QR || EF                       ...`square`

∴ `square/square = square/square                                                           ..."(II)" square`

∴ `square/square = square/square`                                ...from (I) and (II)

∴ seg PR || seg DF           ...(converse of basic proportionality theorem)

In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC. 

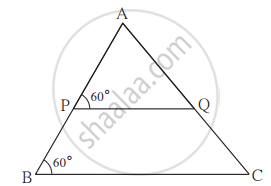
In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Are the triangles in the given figure similar? If yes, by which test? 

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC. 

 In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ 

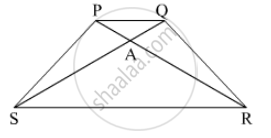
In trapezium ABCD, side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15 then Find OD. 

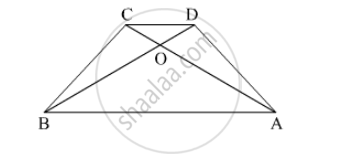
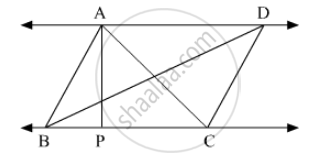
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE. 

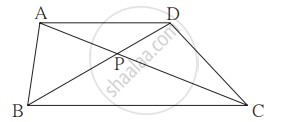
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA² = CB × CD 

The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.

If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks. 

\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]

If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\] 

∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN. 

Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.

∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.

In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity. 

Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\] 

If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

 In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?

∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE? 

In the given figure, seg XY || seg BC, then which of the following statements is true?

In ∆ABC, B - D - C and BD = 7, BC = 20 then find following ratio. 

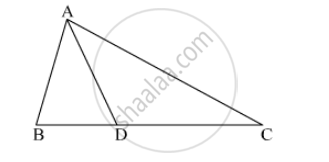
`"A(∆ ABD)"/"A(∆ ADC)"`

In ∆ABC, B – D – C and BD = 7, BC = 20, then find the following ratio.

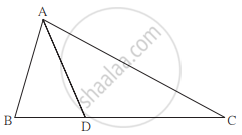
`(A(∆ABD))/(A(∆ABC))`

In ∆ABC, B – D – C and BD = 7, BC = 20 then Find following ratio. 

\[\frac{A\left( ∆ ADC \right)}{A\left( ∆ ABC \right)}\] 

Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?

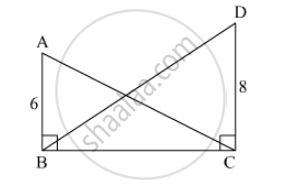
In the given figure, ∠ABC = ∠DCB = 90° AB = 6, DC = 8 then `("A(Δ ABC)")/("A(Δ DCB)")` = ?

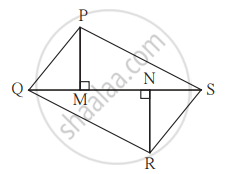
In the figure, PM = 10 cm, A(∆PQS) = 100 sq.cm, A(∆QRS) = 110 sq. cm, then find NR.

∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.

In the given figure, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then Find BE.

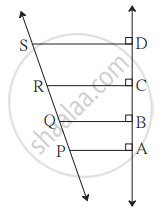
In the given figure, seg PA, seg QB, seg RC, and seg SD are perpendicular to line AD.

AB = 60, BC = 70, CD = 80, PS = 280 then find PQ, QR, and RS. 

In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR. 

Complete the proof by filling in the boxes.

In △PMQ, ray MX is bisector of ∠PMQ.

∴ `square/square = square/square` .......... (I) theorem of angle bisector.

In △PMR, ray MY is bisector of ∠PMQ.

∴ `square/square = square/square` .......... (II) theorem of angle bisector.

But `(MP)/(MQ) = (MP)/(MR)` .......... M is the midpoint QR, hence MQ = MR.

∴ `(PX)/(XQ) = (PY)/(YR)`

∴ XY || QR .......... converse of basic proportionality theorem.

In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find `"AX"/"XY"`.

In ▢ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that `"AP"/"PD" = "PC"/"BP"`.

In the given fig, XY || seg AC. If 2AX = 3BX and XY = 9. Complete the activity to Find the value of AC.  

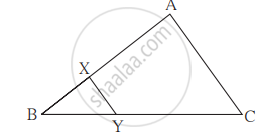
Activity: 2AX = 3BX  

∴ `"AX"/"BX" = square/square`

`("AX" +"BX")/"BX" = (square + square)/square`   ...(by componendo)

`"AB"/"BX" = square/square`           ...(I)

ΔBCA ~ ΔBYX             ...`square` test of similarity,

∴ `"BA"/"BX" = "AC"/"XY"`    ...(corresponding sides of similar triangles)

∴ `square/square = "AC"/9`      

∴ AC = `square`        ...[From(I)]

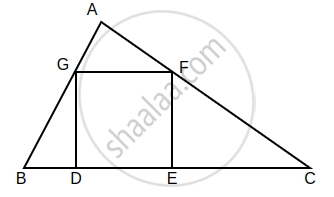
In the given figure, the vertices of square DEFG are on the sides of ∆ABC. ∠A = 90°. Then prove that DE² = BD × EC. (Hint: Show that ∆GBD is similar to ∆CFE. Use GD = FE = DE.)