Advertisements
Advertisements
Question
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
Solution
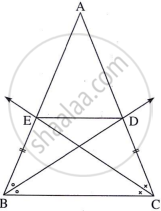
In ΔABC, ray BD is the bisector of ∠ABC
∴ by the theorem of an angle bisector of a triangle,
`"AB"/"BC"="AD"/"DC"` ...(1)
In ΔABC, ray CE is the bisector of ∠ACB
∴ by the theorem of an angle bisector of a triangle,
`"AC"/"BC"="AE"/"EB"` ...(2)
Seg AB ≅ seg AC (Given) ...(3)
[From (1), (2) and (3)]
∴ `"AB"/"BC"="AC"/"BC"` ...(4)
In ΔABC,
`"AE"/"EB"="AD"/"DC"` ...[From (1), (2) and (4)]
∴ by converse of basic proportionality theorem,
seg ED || side BC
∴ ED II BC
APPEARS IN
RELATED QUESTIONS
See the given figure. DE || BC. Find EC.

In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.
prove that
`("AM")/("PN")=("AX")/("PY")`
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
