Advertisements
Advertisements
Question
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
Solution
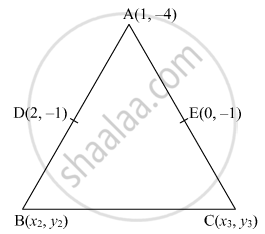
Let D is mid-point of AB and E is the midpoint of AC.
Coordinates of A (1, -4)
Using mid-point `"x" = ("x"_1+"x"_2)/2 , "y" = ("y"_1+"y"_2)/2`
we will find coordinates of B using mid-point in AB
`2 = (1+"x"_2)/2 , -1 = (-4+"y"_2)/2`
`"x"_2 = 3, "y"_2 = 2`
Coordinates of B (3,2)
Now, we will find coordinates of C from mid-point formula in AC
`0 = (1+"x"_3)/2, -1 =(-4+"y"_3)/2`
`"x"_3 = -1, "y"_3 = 2`
Coordinates of C (-1,2)
Now, using coordinates A (1,-4), B(3,2) and C(-1,2) in the formula of area of triangle which is:
`1/2["x"_1("y"_2-"y"_3)+"x"_2("y"_3-"y"_1)+("x"_3("y"_1-"y"_2)]`
`1/2 [1(2-2)+3(2-(-4))+(-1)(-4-2)]`
`=1/2 [0+18+6]`
`1/2(24) = 12 "sq.units"`
APPEARS IN
RELATED QUESTIONS
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
State, true or false:
All isosceles triangles are similar.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
Find the scale factor in each of the following and state the type of size transformation:
Actual length = 12cm, Image length = 15cm.
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
Two similar triangles will always have ________ angles
From the figure, prove that ∆SUN ~ ∆RAY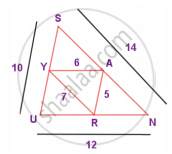
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
