Advertisements
Advertisements
प्रश्न
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
उत्तर
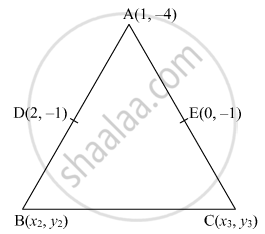
Let D is mid-point of AB and E is the midpoint of AC.
Coordinates of A (1, -4)
Using mid-point `"x" = ("x"_1+"x"_2)/2 , "y" = ("y"_1+"y"_2)/2`
we will find coordinates of B using mid-point in AB
`2 = (1+"x"_2)/2 , -1 = (-4+"y"_2)/2`
`"x"_2 = 3, "y"_2 = 2`
Coordinates of B (3,2)
Now, we will find coordinates of C from mid-point formula in AC
`0 = (1+"x"_3)/2, -1 =(-4+"y"_3)/2`
`"x"_3 = -1, "y"_3 = 2`
Coordinates of C (-1,2)
Now, using coordinates A (1,-4), B(3,2) and C(-1,2) in the formula of area of triangle which is:
`1/2["x"_1("y"_2-"y"_3)+"x"_2("y"_3-"y"_1)+("x"_3("y"_1-"y"_2)]`
`1/2 [1(2-2)+3(2-(-4))+(-1)(-4-2)]`
`=1/2 [0+18+6]`
`1/2(24) = 12 "sq.units"`
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || OQ and DF || OR, show that EF || QR.

`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

State the SAS-similarity criterion
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
Check whether the triangles are similar and find the value of x
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
In ∠BAC = 90° and AD ⊥ BC. A then ______.

In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

