Question

Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)

Answer 1

Given triangle ∆ABC, we are required to construct another triangle whose sides are `6/5` of the corresponding sides of the ∆ABC.

Steps of construction:

(i) Construct an ∆ABC with any measurement.

(ii) Draw a ray BX making an acute angle with BC.

(iii) Locate 6 points Q₁, Q₂, Q₃, Q₄, Q₅, Q₆ on BX such that
BQ₁ = Q₁Q₂ = Q₂Q₃ = Q₃Q₄ = Q₅Q₆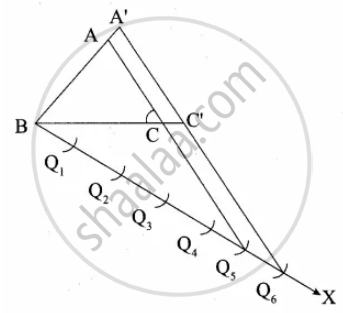  

(iv) Join Q₅ to C and draw a line through Q₆ parallel to Q₅ C intersecting the extended line BC at C’.

(v) Draw a line through C’ parallel to AC intersecting the extended line segment AB at A’.

∴ ∆A’BC’ is the required triangle.