Question

Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)

Answer 1

Given a triangle LMN, we are required to construct another triangle whose sides are `4/5` of the corresponding sides of the ∆LMN.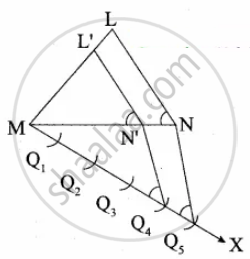

Steps of Construction:

1. Construct a ∆LMN with any measurement.

2. Draw a ray MX making an acute angle with MN on the side opposite to the vertex L.

3. Locate 5 Points Q₁, Q₂, Q₃, Q₄, Q₅ on MX.
So that MQ₁ = Q₁Q₂ = Q₂Q₃ = Q₃Q₄ = Q₄Q₅

4. Join Q₅ N and draw a line through Q₄. Parallel to Q₅ N to intersect MN at N’.

5. Draw a line through N’ parallel to the line LN to intersect ML at L’.

∴ ∆L’MN’ is the required triangle.