Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
उत्तर
Given a triangle LMN, we are required to construct another triangle whose sides are `4/5` of the corresponding sides of the ∆LMN.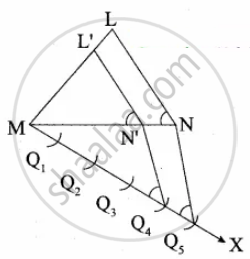
Steps of Construction:
1. Construct a ∆LMN with any measurement.
2. Draw a ray MX making an acute angle with MN on the side opposite to the vertex L.
3. Locate 5 Points Q1, Q2, Q3, Q4, Q5 on MX.
So that MQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q4Q5
4. Join Q5 N and draw a line through Q4. Parallel to Q5 N to intersect MN at N’.
5. Draw a line through N’ parallel to the line LN to intersect ML at L’.
∴ ∆L’MN’ is the required triangle.
APPEARS IN
संबंधित प्रश्न
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
