Advertisements
Advertisements
प्रश्न
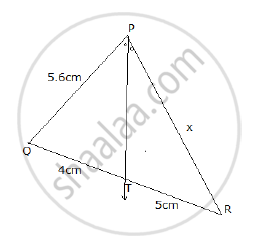
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

उत्तर
Given: ray PT is bisector of ∠QPR.
PQ = 5.6 cm, QT = 4 cm and TR = 5 cm.
In a triangle, the angle bisector divides the side opposite to the angle in the ratio of the remaining sides.
`"QT"/"TR"="PQ"/"PR"`
`4/5=5.6/x`
`x=(5.6xx5)/4`
`x=28/4=7`
`PR=7cm`
APPEARS IN
संबंधित प्रश्न
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
State, true or false:
Two isosceles-right triangles are similar.
State the SSS-similarity criterion for similarity of triangles
State the SAS-similarity criterion
In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"EC"`
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The length of a scale in km represented by 1cm on the map.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN

In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`

In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
