Advertisements
Advertisements
प्रश्न
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
उत्तर
Given: ΔPQR is an equilateral triangle with PQ = QR = PR = 8 cm and ΔABC is an equilateral triangle with AB = BC = AC = 4 cm
To find: A(ΔABC)
Construction: Draw seg AD ⊥ BC, B−D−C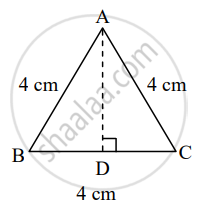
In ΔABD,
∠ADB = 90° ...[Construction]
∠ABD = 60° ...[Angle of an equilateral triangle]
∠BAD = 30° ...[Remaining angle of a triangle]
∴ ΔABD is a 30°–60°–90° triangle.
∴ AD = `sqrt(3)/2` AB ...[Side opposite to 60°]
∴ AD = `sqrt(3)/2 xx 4`
∴ AD = `2sqrt(3)` ...(i)
Area of triangle = `1/2 xx "height" xx "base" `
∴ Area of ΔABC = `1/2 xx "AD" xx "BC"`
= `1/2 xx 2sqrt(3) xx 4`
= `2 xx 2sqrt(3)`
= `4sqrt(3)` ......[From (i)]
∴ Area of the triangle whose side is half of the side of ΔPQR is `4sqrt(3)` sq.cm
APPEARS IN
संबंधित प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
The dimensions of the model of a building are 1.2m x 75cm x 2m. If the scale factor is 1 : 20; find the actual dimensions of the building.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The length of a scale in km represented by 1cm on the map.
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
