Advertisements
Advertisements
प्रश्न
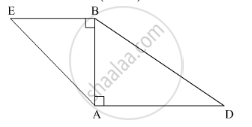
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]
उत्तर

APPEARS IN
संबंधित प्रश्न
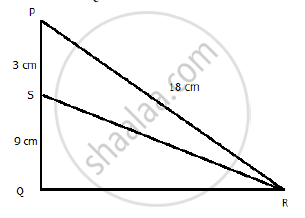
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.
Prove that: PQ2 = PD × PA.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.
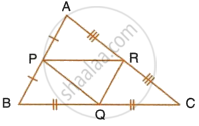
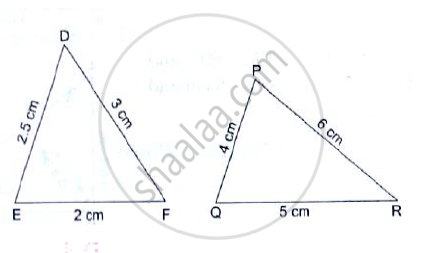
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
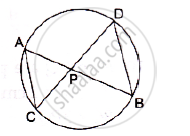
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m3, find the volume of the tank on the top of the model.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
PQ is perpendicular to BA and BD is perpendicular to AP.PQ and BD intersect at R. Prove that ΔABD ∼ ΔAPQ and `"AB"/"AP" = "BD"/"PQ"`.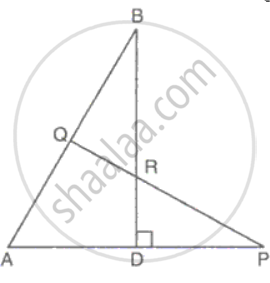
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
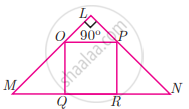
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.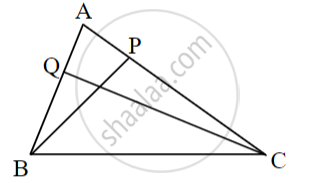
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
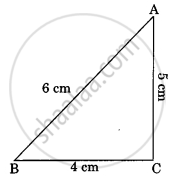
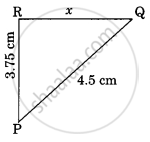
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
