Advertisements
Advertisements
प्रश्न
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

उत्तर
Given : AB and CD are two chords
To Prove:
(a) Δ PAC ~ ΔPDB
(b) PA.PB = PC.PD
Proof: In Δ PAC and Δ PDB
∠𝐴𝑃𝐶 = ∠𝐷𝑃𝐵 (𝑉𝑒𝑟𝑡𝑖𝑐𝑎𝑙𝑙𝑦 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠)
∠𝐶𝐴𝑃 = ∠𝐵𝐷𝑃 (𝐴𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑠𝑎𝑚𝑒 𝑠𝑒𝑔𝑚𝑒𝑛𝑡 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙)
𝑏𝑦 𝐴𝐴 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑐𝑟𝑖𝑡𝑒𝑟𝑖𝑜𝑛 Δ𝑃𝐴𝐶 ~𝑃𝐷𝐵
When two triangles are similar, then the ratios of lengths of their corresponding sides are proportional.
`∴ (PA)/(PD)=(PC)/(PB)`
⟹ PA. PB = PC. PD
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

See the given figure. DE || BC. Find EC.

The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`

The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

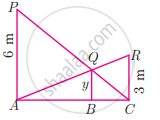
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

Observe the figure and complete the following activity

In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

