Advertisements
Advertisements
प्रश्न
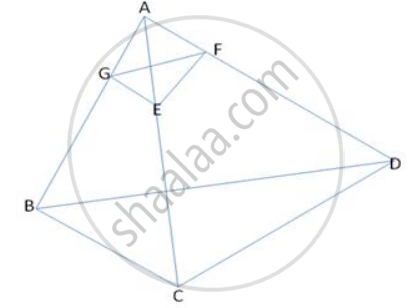
In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`
उत्तर
In Δ ABC, GE || BC
∴ By BPT
`"AG"/"GB" = "AF"/"FD"` .......(1)
Similarly, in Δ ACD
`"AE"/"EC" = "AF"/"FD"` .....(2)
From ( 1) and (2)
`"AG"/"GB" = "AF"/"FD"`
∴ GE || BC ...(By converse of BPT)
In Δ AGF and Δ ABD
∠ A = ∠ A (common)
∠ AFG = ∠ ADB (Corresponding angles)
∴ Δ AGF ∼ Δ ABD (AA corollary)
∴ `"AF"/"AD" = "GF"/"BD"` (Similar sides of similar triangles)
`2.1/7 = "GF"/"BD"`
`3/10 = "GF"/"BD"`
`("Ar" triangle "GEF")/("Ar" triangle "BCD") = "GF"^2/"BD"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
= `(3/10)^2`
= `9/100`
= 9 : 100
`("Ar" triangle "BCD") : ("Ar" triangle "GEF")` = 100 : 9
APPEARS IN
संबंधित प्रश्न
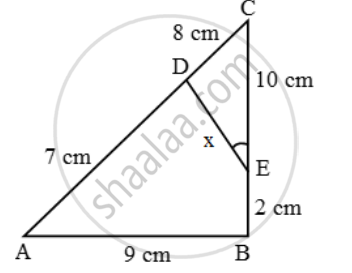
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.
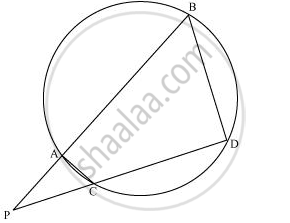
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD
State, true or false:
All isosceles triangles are similar.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
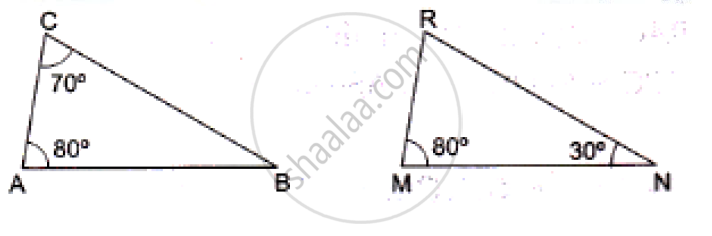
Are the triangles in the given figure similar? If yes, by which test?
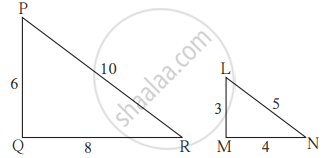
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
From the given figure, prove that ΔABC ~ ΔEDF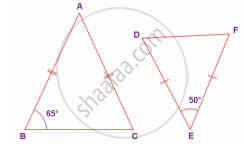
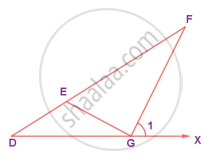
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF