Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
рдЙрддреНрддрд░
In Δ ABC
∠A + ∠ЁЭР╡+ ∠ЁЭР╢=1800 (Angle Sum Property)
тЯ╣80°+ ∠ЁЭР╡+700=180°
тЯ╣ ∠ЁЭР╡=30°
∠ЁЭР┤= ∠ЁЭСА ЁЭСОЁЭСЫЁЭСС ∠ЁЭР╡= ∠ЁЭСБ
Therefore, by AA similarity , Δ ABC - Δ MNR
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
In an isosceles тИЖABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that тИЖACP ~ тИЖBCQ.
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.
Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
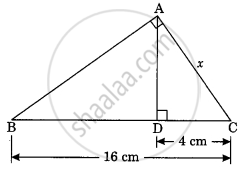
In the given figure, ∠ABC = 90° and BD⊥AC. If BD = 8cm, AD = 4cm, find CD.
In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
An aeroplane is 30m long and its model is l5 cm long. If the total outer surface area of the model is 150 cm2 , find the cost of painting the outer surface of the aeroplane at Rs. 120 per m2, if 5O m2 is left out for windows.
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
Let тИЖ ABC тИ╜ тИЖ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
If тИЖABC – тИЖPQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
In the given figure the value of x is
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.
