Advertisements
Advertisements
प्रश्न
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
उत्तर
Given: △ABC ~ △DEF
We know the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
`("arΔABC")/("arΔDEF") = ("BC"/"EF")^2`
⇒ `64/121 = ("BC"/15.4)^2`
⇒ `(8/11)^2 = ("BC"/15.4)^2`
⇒ `8/11 = "BC"/15.4`
⇒ BC = `(8 xx 15.4)/11` = 11.2 cm
Thus, BC = 11.2 cm.
APPEARS IN
संबंधित प्रश्न
In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

State, true or false:
All equiangular triangles are similar.
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

State the SSS-similarity criterion for similarity of triangles
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
ABCD and PQRS are similar figures. AB= 12cm, BC=x cm, CD= 15 cm, AD= 10 cm, PQ= 8 cm, QR = 5 cm, RS = m cm and PS = n cm .Find the values of x, m and n.
In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
In fig.DE || BC ,AD = 1 cm and BD = 2 cm. what is the ratio of the ar(ΔABC) to the ar (ΔADE)?

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
On a map drawn to a scale of 1: 2,50,000, a triangular plot of land has the following measurements:
AB = 3 cm, BC = 4 cm, ∠ABC = 90°. Calculate:
(i) The actual length of AB in km.
(ii) The area of Plot in sq. km.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

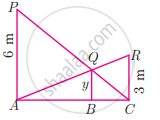
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
