Advertisements
Advertisements
प्रश्न
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
उत्तर
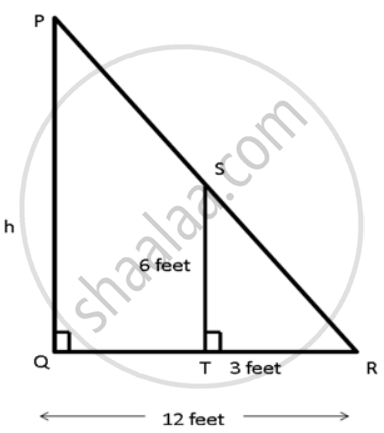
Harmeet and the pole will be perpendicular to the ground.
So, PQ || ST
In ΔPQR and ΔSTR,
∠PQR = ∠STR ...(Both are right angles)
∠PRQ = ∠SRT ...(common angle)
ΔPQR and ΔSTR ...(AA crriterion for similarity)
`"PQ"/"ST" = "QR"/"TR"`
⇒ `"h"/(6) = (12)/(3)`
⇒ h = 24 feet
Hence, the height of the pole is 24 feet.
APPEARS IN
संबंधित प्रश्न
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
Write the test of similarity for triangles given in figure.
