Advertisements
Advertisements
Question
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
Solution
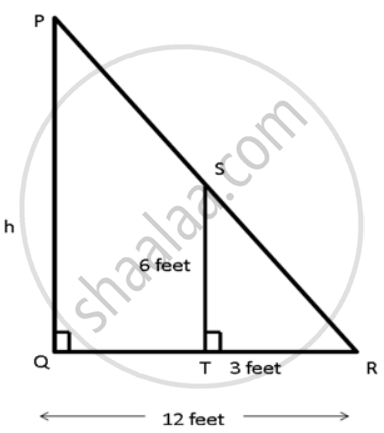
Harmeet and the pole will be perpendicular to the ground.
So, PQ || ST
In ΔPQR and ΔSTR,
∠PQR = ∠STR ...(Both are right angles)
∠PRQ = ∠SRT ...(common angle)
ΔPQR and ΔSTR ...(AA crriterion for similarity)
`"PQ"/"ST" = "QR"/"TR"`
⇒ `"h"/(6) = (12)/(3)`
⇒ h = 24 feet
Hence, the height of the pole is 24 feet.
APPEARS IN
RELATED QUESTIONS
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
State, true or false:
All equiangular triangles are similar.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.

The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
ΔABC and ΔBDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of triangle ΔABC and ΔBDE is ______.
