Advertisements
Advertisements
Question
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
Solution
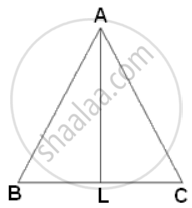
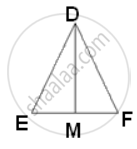
The ratio of the areas of two similar triangles is equal to the ratio of the square of the corresponding altitudes.
∴ `("area"(Δ"ABC"))/("area"(Δ"PQR")) = "AL"^2/"DM"^2`
⇒ `(16)/(9) = "AL"^2/1.8^2`
⇒ AL2 = `(16 xx 3.24)/(9)`
⇒ AL2 = 5.76
⇒ AL = 2.4cm.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∆ABC and ∆AMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
- Prove that: ∆ABC ~ ∆AMP
- Find: AB and BC.

∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
Write the test of similarity for triangles given in figure.
In the adjoining diagram the length of PR is ______.

