Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
उत्तर
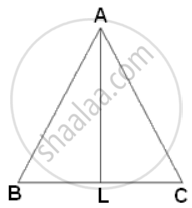
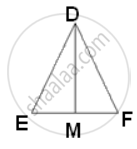
The ratio of the areas of two similar triangles is equal to the ratio of the square of the corresponding altitudes.
∴ `("area"(Δ"ABC"))/("area"(Δ"PQR")) = "AL"^2/"DM"^2`
⇒ `(16)/(9) = "AL"^2/1.8^2`
⇒ AL2 = `(16 xx 3.24)/(9)`
⇒ AL2 = 5.76
⇒ AL = 2.4cm.
APPEARS IN
संबंधित प्रश्न
See the given figure. DE || BC. Find EC.

ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.

The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Two similar triangles will always have ________ angles
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
