Advertisements
Advertisements
प्रश्न
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
उत्तर
Let the height of the tree AD be “h”.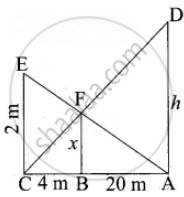
In ∆ACD and ∆BCF,
∠A = ∠B = 90°
∠C is common
∆ACD ~ ∆BCF by AA similarity
`"AD"/"BF" = "AC"/"BC"`
`"h"/x = 24/2` = 6
h = 6x ...(1)
In ∆ACE and ∆ABF,
∠C = ∠B = 90°
∠A is common
∴ ∆ACE ~ ∆ABF
`"CE"/"BF" = "AC"/"AB"`
`2/x = 24/20`
24x = 20 × 2
x = `(20 xx 2)/24 = (5 xx 2)/6 = 10/6`
x = `5/3`
Substitute the value of x in (1)
h = `6 xx 5/3` = 10 m
∴ Height of the tree is 10 m
APPEARS IN
संबंधित प्रश्न
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that TP:TQ = TR:TS
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The number of KM represented by 2cm on the map.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The actual length of the sides in km
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
