Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
उत्तर
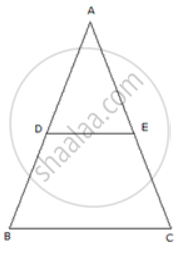
Area(ΔADE) = area(trapezium BCED)
⇒ Area(ΔADE) + Area(ΔADE)
= Area(trapezium BCED) + Area(ΔADE)
⇒ 2 Area(ΔADE) = Area(ΔABC)
In ΔADE and ΔABC,
∠ADE = ∠B ...(corresponding angles)
∠A = ∠A
Therefore, ΔADE ∼ ΔABC
∴ `"area(Δ ADE)"/"area(Δ ABC)" = "AD"^2/"AB"^2`
⇒ `"area(ΔADE)"/(2" x area(ΔADE)") = "AD"^2/"AB"^2`
⇒ `(1)/(2) = ("AD"/"AB")^2`
⇒ `"AD"/"AB" = (1)/sqrt(2)`
⇒ AB = `sqrt(2)"AD"`
⇒ AB = `sqrt(2)("AB - BD")`
⇒ `(sqrt(2) - 1)"AB" = sqrt(2)"BD"`
⇒ `"BD"/"AB" = (sqrt(2) - 1)/(sqrt(2)`
= `(2 - sqrt(2))/(2)`.
APPEARS IN
संबंधित प्रश्न
In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
