Advertisements
Advertisements
प्रश्न
In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
उत्तर

Since, `"AB"/"DE"="BC"/"EF"="AC"/"DE"=1/2`
Then, ΔABC ~ ΔDEF [By SSS similarity]
Now, In ΔABL ~ ΔDEM
∠B = ∠E [Δ ABC ~ ΔDEF]
∠ALB = ∠DME [Each 90°]
Then, ΔABL ~ ΔDEM [By AA similarity]
`therefore"AB"/"DE"="AL"/"DM"` [Corresponding parts of similar Δ are proportional]
`rArr5/10="AL"/"DM"`
`rArr1/2="AL"/"DM"`
APPEARS IN
संबंधित प्रश्न
In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
The two similar triangles are equal in area. Prove that the triangles are congruent.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
In Δ ABC , MN || BC .

If `"AB"/"AM" = 9/4` , find `("Ar" ("trapezium MBCN"))/("Ar" . (triangle "ABC"))`
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m3, find the volume of the tank on the top of the model.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
From the figure, prove that ∆SUN ~ ∆RAY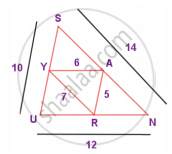
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
In ∠BAC = 90° and AD ⊥ BC. A then ______.

If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
