Advertisements
Advertisements
प्रश्न
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
उत्तर
(i) Here k = `(1)/(2,50,000)`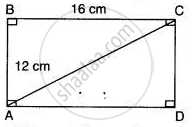
Length of diagonal (on map)
= `sqrt("AB"^2 + "BC"^2)`
= `sqrt(12^2 + 16^2)`
= `sqrt(400)`
= 20 cm
(ii) Length of diagonal on map
= k x Actual length of the diagonal
⇒ 20 = `(1)/(2,50,000) xx "Actual length of the diagonal"`
⇒ Actual length of diagonal
= 20 (2,50,000) cm
= 5000000 cm
= 50 km.
APPEARS IN
संबंधित प्रश्न
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.
prove that
`("AM")/("PN")=("AX")/("PY")`
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
The dimensions of the model of a building are 1.2m x 75cm x 2m. If the scale factor is 1 : 20; find the actual dimensions of the building.
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
