Advertisements
Advertisements
Question
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
Solution
(i) Here k = `(1)/(2,50,000)`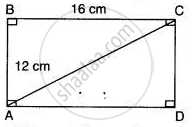
Length of diagonal (on map)
= `sqrt("AB"^2 + "BC"^2)`
= `sqrt(12^2 + 16^2)`
= `sqrt(400)`
= 20 cm
(ii) Length of diagonal on map
= k x Actual length of the diagonal
⇒ 20 = `(1)/(2,50,000) xx "Actual length of the diagonal"`
⇒ Actual length of diagonal
= 20 (2,50,000) cm
= 5000000 cm
= 50 km.
APPEARS IN
RELATED QUESTIONS
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The ground area in km2 that is represented by 2cm2 on the map.
A model of a ship is made to a scale of 1:500. Find: The length of the ship, if length of the model is 1.2.
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ

PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

