Advertisements
Advertisements
Question
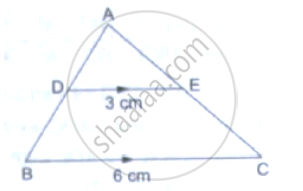
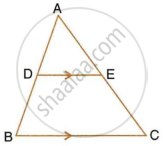
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.
Solution
It is given that DE || BC
∴ ∠𝐴𝐷𝐸= ∠𝐴𝐵𝐶 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠)
∠𝐴𝐸𝐷= ∠𝐴𝐶𝐵 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠)
By AA similarity, we can conclude that Δ ADE ~ Δ ABC
`(ar(ΔADE))/(ar(ΔABC))=(DE)^2/(BC)^2`
⇒ `15/(ar(ΔABC))=3^2/6^2`
⇒ `ar(ΔABC)=(15xx36)/9`
= `60cm^2`
Hence, area of triangle ABC is `60 cm^2`
APPEARS IN
RELATED QUESTIONS
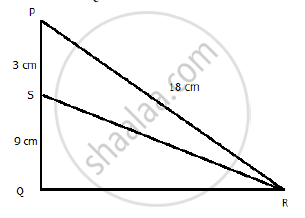
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.
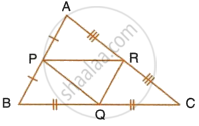
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.
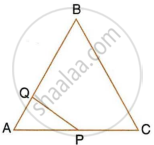
Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
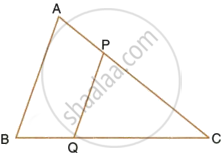
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.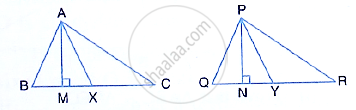
prove that
`("AM")/("PN")=("AX")/("PY")`
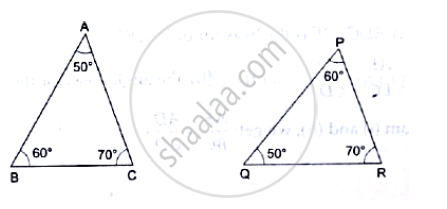
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
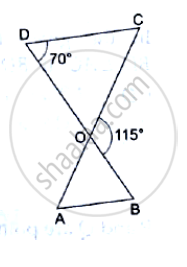
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.
A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.
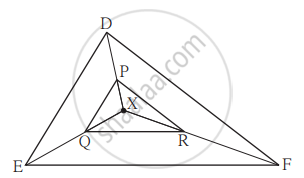
Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
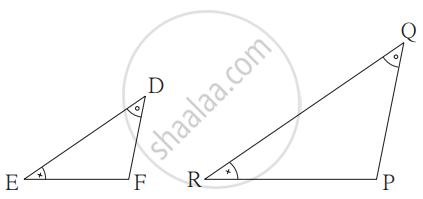
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?
Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : If AP = x, then the value of AC in terms of x.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.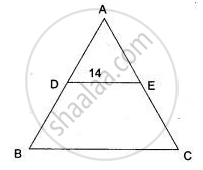
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.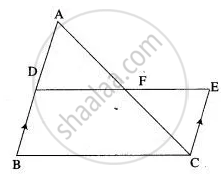
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 10.8cm, BD = 4.5cm, AC = 4.8cm, and AE = 2.8cm
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.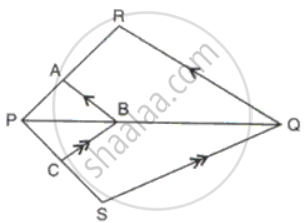
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
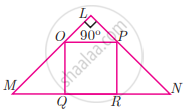
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN
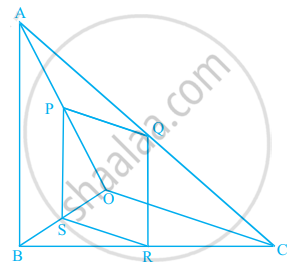
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
Which of the following is not a test of similarity?
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.