Advertisements
Advertisements
Question
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.

Solution
i. Given that `(AD)/(DB) = 3/5`
Now, DE is parallel to BC.
Then, by basic proportionality theorem, we have
`(AD)/(DB) = (AE)/(EC)`
`=> (AE)/(EC) = 3/5`
ii. Given that `(AD)/(DB) = 3/5`
So, `(AD)/(AB) = 3/8`
iii. Given that `(AD)/(DB) = 3/5`
So, `(AD)/(AB) = 3/8`
In ΔADE and ΔABC,
∠ADE = ∠ABC ...(Since DE || BC, so the angles are corresponding angles)
∠A = ∠A ...(Common angle)
∴ ΔADE ∼ ΔABC ...(AA criterion for similarity)
`=> (AD)/(AB) = (AE)/(AC)`
`=> (AE)/(AC) = 3/8`
iv. Given that `(AD)/(DB) = 3/5`
So, `(AD)/(AB) = 3/8`
In ΔADE and ΔABC,
∠ADE = ∠ABC ...(Since DE || BC, so the angles are corresponding angles)
∠A = ∠A ...(Common angle)
∴ ΔADE ∼ ΔABC ...(AA criterion for similarity)
`=> (AD)/(AB) = (DE)/(BC)`
`=> 3/8 = (2.4)/(BC)`
`=>` BC = 6.4 cm
v. Given that `(AD)/(DB) = 3/5`
So, `(AD)/(AB) = 3/8`
In ΔADE and ΔABC,
∠ADE = ∠ABC ...(Since DE || BC, so the angles are corresponding angles)
∠A = ∠A ...(Common angle)
∴ ΔADE ∼ ΔABC ...(AA criterion for similarity)
`=> (AD)/(AB) = (DE)/(BC)`
`=> 3/8 = (DE)/(4.8)`
`=>` DE = 1.8 cm
APPEARS IN
RELATED QUESTIONS
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
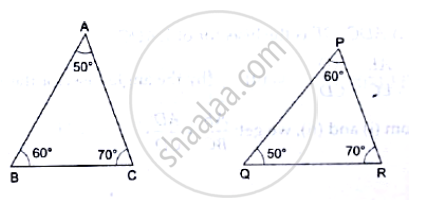
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
ΔPQR ~ ΔSUV. Write pairs of congruent angles
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
