Advertisements
Advertisements
Question
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
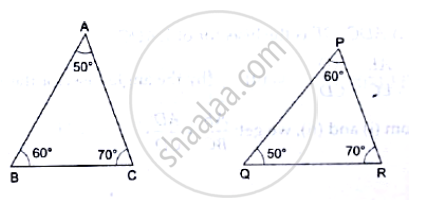
Solution
We have:
∠BAC = ∠PQR = 500
∠ABC = ∠QPR = 600
∠ACB = ∠PRQ = 700
Therefore, by AAA similarity theorem, Δ ABC – QPR
APPEARS IN
RELATED QUESTIONS
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
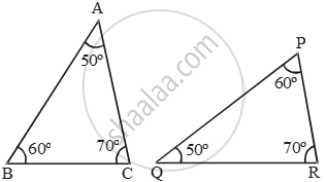
figure (i)
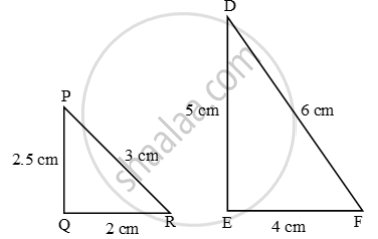
figure 2
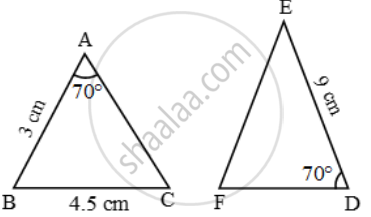
figure 3

figure 4
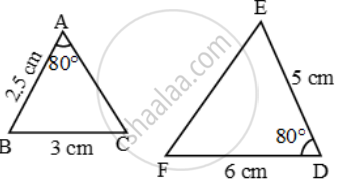
figure 5
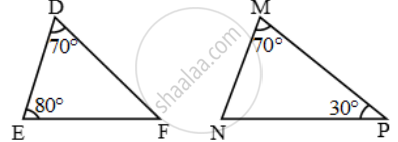
figure 6

figure 7
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ΔAPQ is 116 of the area of ΔABC.
In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
In the figure, which of the following statements is true?
From the figure, prove that ∆SUN ~ ∆RAY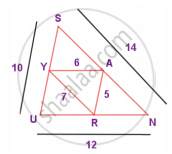
In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

