Advertisements
Advertisements
Question
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
Solution
Given ∠AED = 90°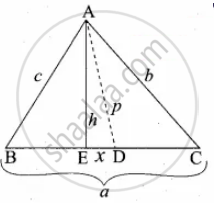
ED = x, DC = `"a"/2` ...(D is the mid point of BC)
∴ EC = `x + "a"/2`, BE = `"a"/2 - x`
∴ In the right ∆AED
AD2 = AE2 + ED2
p2 = h2 + x2
In the right ∆AEC,
AC2 = AE2 + EC2
b2 = `"h"^2 + (x + "a"/2)^2`
= `"h"^2 + x^2 + "a"^2/4 + 2 xx x xx "a"/2`
b2 = `"p"^2 + "a"^2/4 + "a"x`
b2 = `"p"^2 + "a"x + 1/4 "a"^2`
APPEARS IN
RELATED QUESTIONS
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

State the SSS-similarity criterion for similarity of triangles
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
In a square of side 10 cm, its diagonal = ______.
