Advertisements
Chapters
![Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 4 - Geometry Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 4 - Geometry - Shaalaa.com](/images/mathematics-english-class-10-sslc-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 4: Geometry
Below listed, you can find solutions for Chapter 4 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics [English] Class 10 SSLC TN Board.
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Exercise 4.1 [Pages 170 - 171]
Check whether the triangles are similar and find the value of x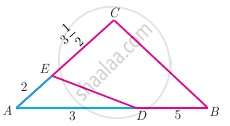
Check whether the triangles are similar and find the value of x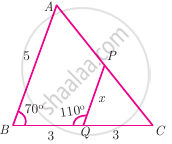
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE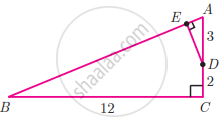
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ
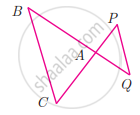
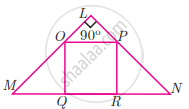
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN
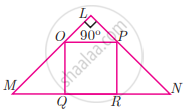
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN
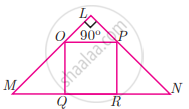
If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
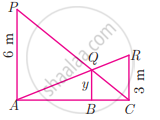
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Exercise 4.2 [Pages 181 - 183]
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB" = 3/4` and AC = 15 cm find AE
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x – 7, DB = 5x – 3, AE = 4x – 3 and EC = 3x – 1, find the value of x
ABCD is a trapezium in which AB || DC and P, Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.
If PQ || BC and PR || CD prove that `"AR"/"AD" = "AQ"/"AB"`
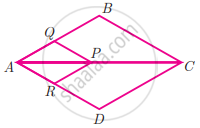
If PQ || BC and PR || CD prove that `"QB"/"AQ" = "DR"/"AR"`
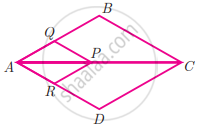
Rhombus PQRB is inscribed in ΔABC such that ∠B is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus.
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that = `"AE"/"ED" = "BF"/"FC"`
DE || BC and CD || EE Prove that AD2 = AB × AF
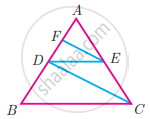
Check whether AD is bisector of ∠A of ∆ABC of the following
AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm
Check whether AD is bisector of ∠A of ∆ABC of the following
AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm.
∠QPR = 90°, PS is its bisector. If ST ⊥ PR, prove that ST × (PQ + PR) = PQ × PR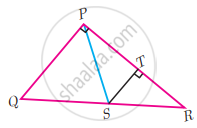
ABCD is a quadrilateral in which AB = AD, the bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
Construct a ∆PQR in which the base PQ = 4.5 cm, ∠R = 35° and the median from R to RG is 6 cm.
Construct a ∆PQR in which QR = 5 cm, ∠P = 40° and the median PG from P to QR is 4.4 cm. Find the length of the altitude from P to QR.
Construct a ∆PQR such that QR = 6.5 cm, ∠P = 60° and the altitude from P to QR is of length 4.5 cm
Construct a ∆ABC such that AB = 5.5 cm, ∠C = 25° and the altitude from C to AB is 4 cm
Draw a triangle ABC of base BC = 5.6 cm, ∠A = 40° and the bisector of ∠A meets BC at D such that CD = 4 cm
Draw ∆PQR such that PQ = 6.8 cm, vertical angle is 50° and the bisector of the vertical angle meets the base at D where PD = 5.2 cm
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Exercise 4.3 [Pages 187 - 188]
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
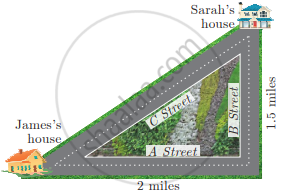
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?

The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
In the adjacent figure, ABC is a right angled triangle with right angle at B and points D, E trisect BC. Prove that 8AE2 = 3AC2 + 5AD2

Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Exercise 4.4 [Pages 198 - 199]
The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?
∆LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
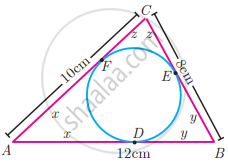
A circle is inscribed in ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure, Find AD, BE and CF.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°. Find ∠OPQ.
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
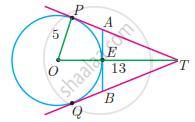
O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.
In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
Show that the angle bisectors of a triangle are concurrent
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure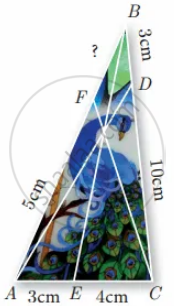
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P?
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Exercise 4.5 [Pages 199 - 200]
Multiple choice questions
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
∠B = ∠E
∠A = ∠D
∠B = ∠D
∠A = ∠F
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
40°
70°
30°
110°
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
2.5 cm
5 cm
10 cm
`5sqrt(2) "cm"`
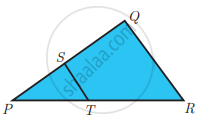
ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is
25 : 4
25 : 7
25 : 11
25 : 13
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
`6 2/3` cm
`(10sqrt(6))/3` cm
`66 2/3` cm
15 cm
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is
1.4 cm
1.8 cm
1.2 cm
1.05 cm
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
6 cm
4 cm
3 cm
8 cm
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then
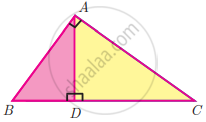
BD.CD = BC2
AB.AC = BC2
BD.CD = AD2
AB.AC = AD2
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
13 m
14 m
15 m
12.8 m
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR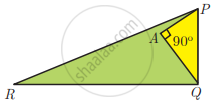
80°
85°
75°
90°
A tangent is perpendicular to the radius at the
centre
point of contact
infinity
chord
How many tangents can be drawn to the circle from an exterior point?
one
two
infinite
zero
The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is
100°
110°
120°
130°
CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is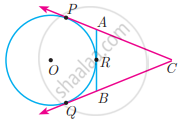
6 cm
5 cm
8 cm
4 cm
If PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is
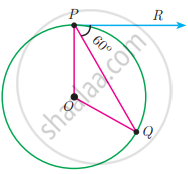
120°
100°
110°
90°
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 4 Geometry Unit Exercise – 4 [Pages 200 - 201]
If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB
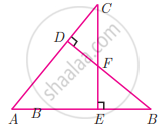
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`
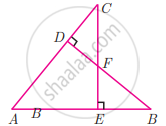
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.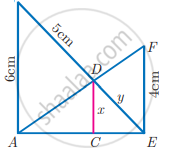
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA
ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle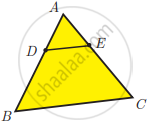
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
An Emu which is 8 feet tall is standing at the foot of a pillar which is 30 feet high. It walks away from the pillar. The shadow of the Emu falls beyond Emu. What is the relation between the length of the shadow and the distance from the Emu to the pillar?
Two circles intersect at A and B. From a point, P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC or their extensions. Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21 . Find the length of the line segment CF
Solutions for 4: Geometry
![Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 4 - Geometry Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 4 - Geometry - Shaalaa.com](/images/mathematics-english-class-10-sslc-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 4 - Geometry
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education 4 (Geometry) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 10 SSLC TN Board chapter 4 Geometry are Thales Theorem and Angle Bisector Theorem, Converse of Pythagoras Theorem, Circles and Tangents, Concurrency Theorems, Similarity of Triangles, Right-angled Triangles and Pythagoras Property, Introduction to Basic Concepts in Geometry.
Using Samacheer Kalvi Mathematics [English] Class 10 SSLC TN Board solutions Geometry exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics [English] Class 10 SSLC TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 4, Geometry Mathematics [English] Class 10 SSLC TN Board additional questions for Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
