Advertisements
Advertisements
Question
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°. Find ∠OPQ.
Solution
∠POQ = 180° – 120° = 60°
In ∆OPQ, we know
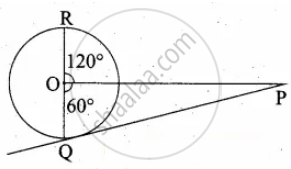
∠POQ + ∠OQP + ∠OPQ = 180° ...(Sum of the angles of a ∆ is 180°)
60° + 90° + ∠OPQ = 180°
∠OPQ = 180° – 150° = 30°
∠OPQ = 30°
APPEARS IN
RELATED QUESTIONS
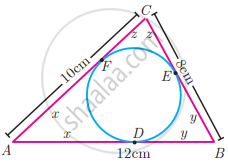
A circle is inscribed in ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure, Find AD, BE and CF.
In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P?
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is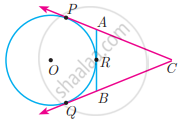
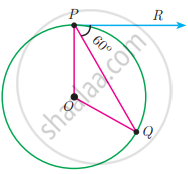
If PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is