Advertisements
Advertisements
Question
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
Solution
Radius of the circle = 4.5 cm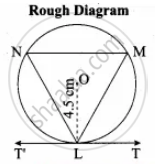
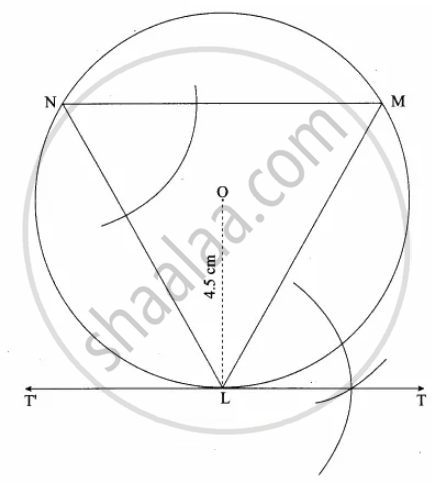
Steps of construction:
1. With O as centre, draw a circle of radius 4.5 cm.
2. Take a point L on the circle. Through L draw any chord LM.
3. Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
4. Through “L” draw tangent TT’such that ∠TLM = ∠MNL
5. TT’ is the required tangent.
APPEARS IN
RELATED QUESTIONS
∆LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
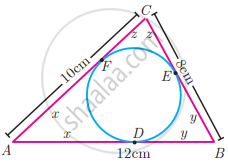
A circle is inscribed in ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure, Find AD, BE and CF.
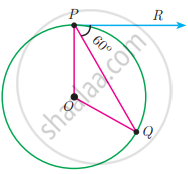
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°. Find ∠OPQ.
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
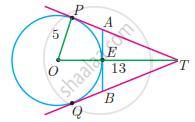
O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P?
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
If PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is