Advertisements
Advertisements
प्रश्न
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
उत्तर
Radius of the circle = 4.5 cm
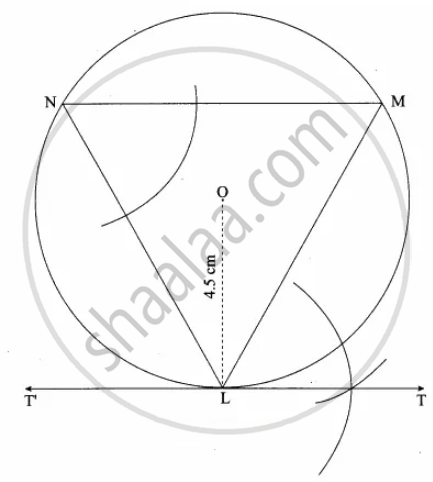
Steps of construction:
1. With O as centre, draw a circle of radius 4.5 cm.
2. Take a point L on the circle. Through L draw any chord LM.
3. Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
4. Through “L” draw tangent TT’such that ∠TLM = ∠MNL
5. TT’ is the required tangent.
APPEARS IN
संबंधित प्रश्न
∆LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
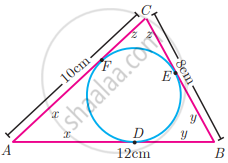
A circle is inscribed in ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure, Find AD, BE and CF.
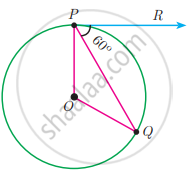
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°. Find ∠OPQ.
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
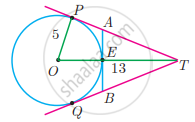
O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
How many tangents can be drawn to the circle from an exterior point?
The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is
CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is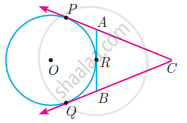
If PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is