Advertisements
Advertisements
Question
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
Solution
A is the position of the 1st train.
B is the position of the 2nd train.
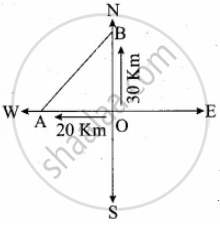
Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours
AB = `sqrt("OA"^2 + "OB"^2)`
= `sqrt(40^2 + 60^2)`
= `sqrt(1600 + 3600)`
= `sqrt(5200)` or `sqrt(52 xx 100)`
= `10sqrt(4 xx 13)`
= `20sqrt(13)`
= 72.11 km
Distance between the two train = 72.11 km or `20sqrt(13) "km"`
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
