Advertisements
Advertisements
Question
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Solution
∆ ABD
∠ACB = ∠ACD = 90°
and AB = 10 cm, BC = 6 cm and AD = 17 cm
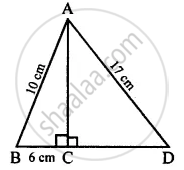
To find:
(i) Length of AC
(ii) Length of CD
Proof:
(i) In right-angled triangle ABC
BC = 6 cm, AB = 110 cm
According to Pythagoras Theorem,
AB2 = AC2 + BC2
(10)2 = (AC)2 + (6)2
100 = (AC)2 + 36
AC2 = 100 − 36 = 64 cm
AC2 = 64 cm
∴ AC = `sqrt(8xx8)` = 8 cm
(ii) In right-angle triangle ACD
AD = 17 cm, AC = 8 cm
According to Pythagoras Theorem,
(AD)2 = (AC)2 + (CD)2
(17)2 = (8)2 + (CD)2
289 – 64 = CD2
225 = CD2
CD =`sqrt(15xx15)` = 15 cm
APPEARS IN
RELATED QUESTIONS
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
