Advertisements
Advertisements
Question
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
Solution
Let l be the length of the longer side and b be the length of the shorter side.
Given that the length of the diagonal of the rectangular field is 16 metres more than the shorter side.
Thus, diagonal = 16 + b
Since longer side is 14 metres more than shorter side, we have,
l= 14 + b
Diagonal is the hypotenuse of the triangle.
Consider the following figure of the rectangular field.
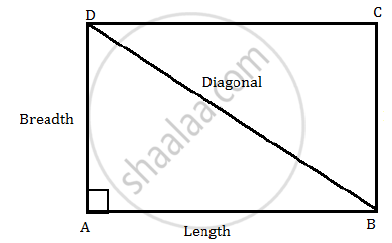
By applying Pythagoras Theorem in ΔABD, we have,
Diagonal2= Length2 +Breadt2
`(16+b)^2=(14+b)^2+b^2`
`256+b^2+32b=196+b^2+28b+b^2`
`256+32b=196+28b+b^2`
`b^2-4b-60=0`
`b^2-10b+6b-60=0`
b(b-10)+6(b-10)=0
(b+6)(b-10)=0
b=-6,b=10
As breadth cannot be negative, breadth = 10 m
Thus, length of the rectangular field = 14 + 10 = 24 m
APPEARS IN
RELATED QUESTIONS
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
