Advertisements
Advertisements
Question
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

Solution
Given : AC = 12 m
BD = 9 m
PA = PB= 15 m
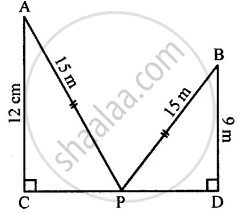
(i) In right angle triangle ACP
(AP)2 = (AC)2 + (CP)2
152 = 122 + CP2
225 = 144 + CP2
225 – 144 = CP2
81 = CP
∴ CP = 9 m
(ii) In right angle triangle BPD
(PB)2 = (BD)2 + (PD)2
(15)2 = (9)2 + PD2
225 = 81 + PD2
225 – 81 = PD2
144 = PD2
∴ PD = 12 m
(iii) CP = 9 m
PD = 12 m
∴ CD = CP + PD
= 9 + 12
= 21 m
APPEARS IN
RELATED QUESTIONS
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Find the side and perimeter of a square whose diagonal is 10 cm.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
Two squares are congruent, if they have same ______.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
