Advertisements
Advertisements
प्रश्न
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD
Advertisements
उत्तर
Given : AC = 12 m
BD = 9 m
PA = PB= 15 m
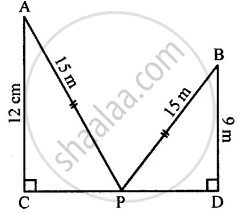
(i) In right angle triangle ACP
(AP)2 = (AC)2 + (CP)2
152 = 122 + CP2
225 = 144 + CP2
225 – 144 = CP2
81 = CP
`sqrt81` = CP
∴ CP = 9 m
(ii) In right angle triangle BPD
(PB)2 = (BD)2 + (PD)2
(15)2 = (9)2 + PD2
225 = 81 + PD2
225 – 81 = PD2
144 = PD2
`sqrt144` = PD2
∴ PD = 12 m
(iii) CP = 9 m
PD = 12 m
∴ CD = CP + PD
= 9 + 12
= 21 m
APPEARS IN
संबंधित प्रश्न
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
