Advertisements
Advertisements
प्रश्न
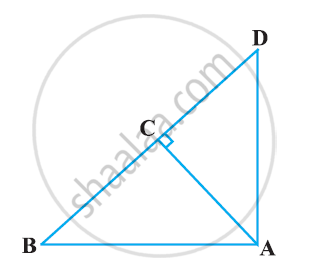
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD
उत्तर
In ΔDCA and ΔDAB, we have
∠DCA = ∠DAB (Each equals to 90°)
∠CDA = ∠ADB (common angle)
∴ ΔDCA ~ ΔDAB [By AA similarity criterion]
`⇒ (DC)/(DA) = (DA)/(DA)`
⇒ AD2 = BD × CD
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
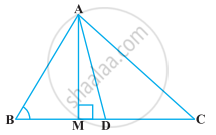
`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
