Advertisements
Advertisements
प्रश्न
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
उत्तर
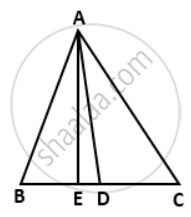
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
In ΔADC, ∠ADC is an obtuse angle.
∴ AC2 = AD2 + DC2 + 2 x DC x DE
⇒ AC2 = AD2 + `(1/2"BC")^2 + 2 xx (1)/(2)"BC" xx "DE"`
⇒ AC2 = AD2 + `(1)/(4)"BC"^2 + "BC" xx "DE"`
⇒ AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2` . ....(i)
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
