Advertisements
Advertisements
प्रश्न
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
उत्तर
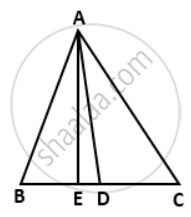
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
In ΔADC, ∠ADC is an obtuse angle.
∴ AC2 = AD2 + DC2 + 2 x DC x DE
⇒ AC2 = AD2 + `(1/2"BC")^2 + 2 xx (1)/(2)"BC" xx "DE"`
⇒ AC2 = AD2 + `(1)/(4)"BC"^2 + "BC" xx "DE"`
⇒ AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2` . ....(i)
APPEARS IN
संबंधित प्रश्न
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Find the side of the square whose diagonal is `16sqrt(2)` cm.
Find the value of (sin2 33 + sin2 57°)
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
