Advertisements
Advertisements
प्रश्न
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

उत्तर
Given that: CD ⊥ AB
∠ACB = 90°
To prove : CD2 = BD × AD
Using pythagoras Theorem in Δ ACD
AC2 = AD2 +CD2 ..........(1)
Using pythagoras Theorem in ΔCDB
CB2 = BD2+CD2 .....(2)
Similarly in ΔABC,
As AB = AD + DB
Since ,AB = AD +BD ......(4)
Squaring both sides of equation (4), we get
(AB)2 = (AD+BD)2
Since, AB2 = AD2 +BD2 +2×BD×AD
From equation (3) we get
AC2 +BC2=AD2+BD2+2 × BD × AD
Substituting the value of AC2 from equation (1) and the value of BC2 from equation (2), we get
AD2 +CD2 +BD2 + CD2 +AD2 +BD2 +2×BD×AD
Since ,2 CD2 = 2 × BD × AD
Hence , CD2 = BD × AD
APPEARS IN
संबंधित प्रश्न
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

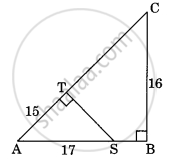
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Two squares are congruent, if they have same ______.
