Advertisements
Advertisements
प्रश्न
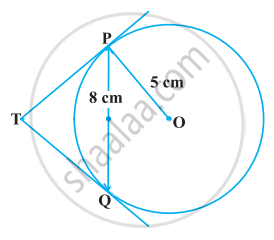
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
उत्तर
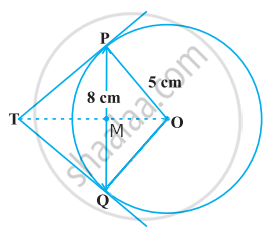
Given radius, OP = OQ = 5 cm
Length of the chord, PQ = 8 cm
OT ⊥ PQ,
∴ PM = MQ = 4 cm ......[Perpendicular draw from the centre of the circle to a chord bisect the chord]
In right ΔOPM,
OP2 = PM2 + OM2
⇒ 52 = 42 + OM2
⇒ OM2 = 25 – 16 = 9
Hence OM = 3 cm
In right ΔPTM,
PT2 = TM2 + PM2 ......(1)
∠OPT = 90° ......[Radius is perpendicular to the tangent at the point of contact]
In right ΔOPT,
OT2 = PT2 + OP2 ......(2)
From equations (1) and (2), we get
OT2 = (TM2 + PM2) + OP2
⇒ (TM + OM)2 = (TM2 + PM2) + OP2
⇒ TM2 + OM2 + 2 × TM × OM = TM2 + PM2 + QP2
⇒ OM2 + 2 × TM × OM = PM2 + OP2
⇒ 9 + 6TM = 16 + 25
⇒ 6TM = 32
⇒ TM = `32/6 = 16/3`
Equation(1) becomes,
PT2 = TM2 + PM2
= `(16/3)^2 + 4^2`
= `(256/9) + 16`
= `(256 + 144)/9`
= `(400/9)`
= `(20/3)^2`
PT = `20/3`
This gives `("TP")/("PO") = ("RP")/("RO")`, i.e., `("TP")/5 = 4/3` or TP = `20/3` cm.
संबंधित प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
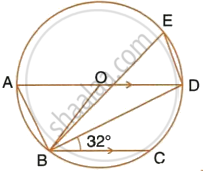
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
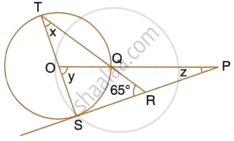
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

